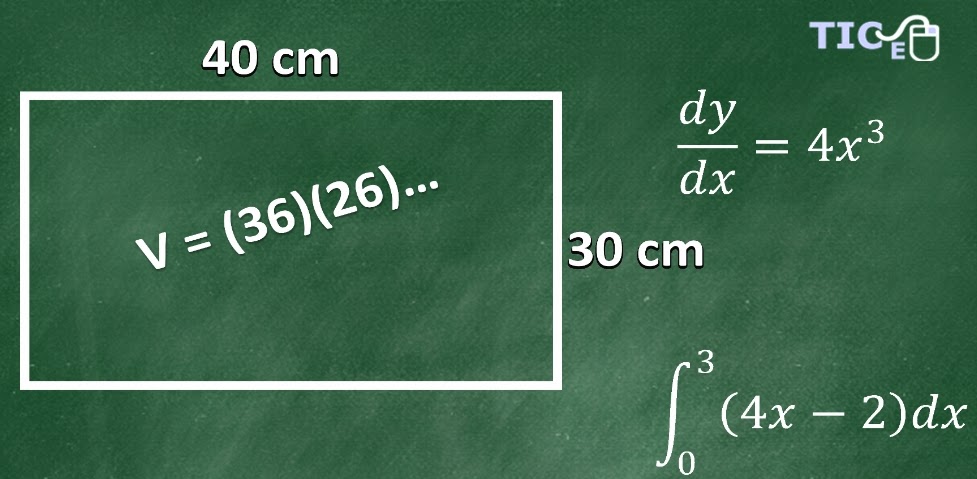Esperamos que sea de utilidad.
Saludos.
La presentación adjunta contiene el encuadre del curso y las indicaciones generales para su seguimiento.
Esperamos que sea de utilidad.
Saludos.
La presentación adjunta contiene el encuadre del curso: Cálculo Diferencial.
Esperamos que sea de utilidad.
Saludos.
La Teoría de Límites es la respuesta a los cuestionamientos que, en un principio, sufrió el cálculo diferencial por el uso de infinitésimos sin un buena fundamento de los mismos. Es la base del cálculo diferencial e integral.
La siguiente actividad tiene la finalidad de introducir este concepto a partir de una situación práctica pasando posteriormente al concepto matemático.
Esperamos que sea de utilidad.
Saludos.
La matemática en general, y el cálculo diferencial en particular, son consideradas herramientas para resolver problemas; aunque tienen un valor intrínseco, a la mayor parte de los profesionistas les interesan sus aplicaciones.
La siguiente presentación contiene una explicación de la forma en que se elabora un modelo matemático a partir de un sencillo problema práctico; la fabricación de una caja de cartón a partir de una pieza rectangular de dicho material.
Esperamos que sea de utilidad,
Saludos.
La siguiente presentación contiene el encuadre del curso de cálculo diferencial con el enfoque de educación basada en competencias.
Esperamos que sea de utilidad.
Saludos.
El cálculo diferencial es una herramienta para resolver problemas, en la siguiente presentación se explica, paso a paso, el procedimiento empleado para plantear y resolver un problema de optimización de recursos.
Esperamos que sea de utilidad.
Saludos.
