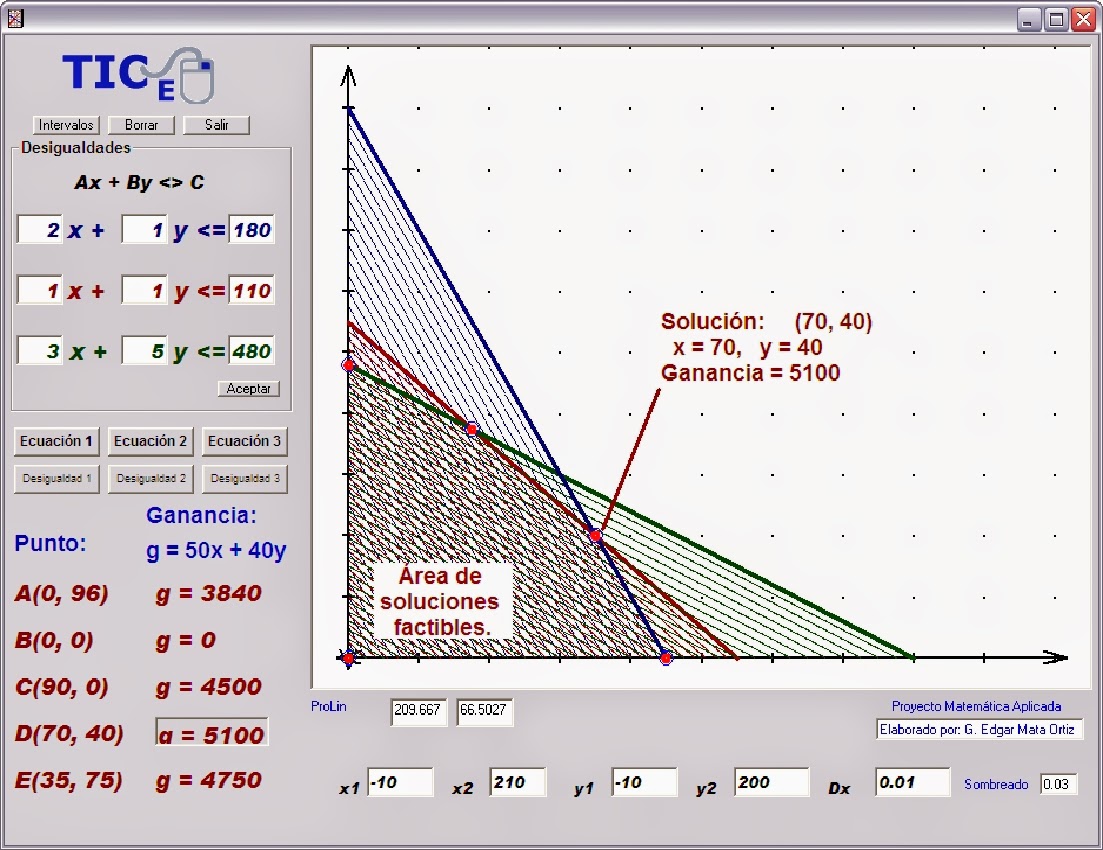
Modelos matemáticos. Plantilla para resolver problemas de programación lineal.
Los
problemas de razonamiento de cualquier área de la matemática o ingeniería suelen representar un desafío para la mayoría de los estudiantes de cualquier nivel escolar.
Una buena parte de la dificultad que enfrentan es la falta de orden en sus procesos de solución, lo cuál ocasiona que, fácilmente, omiten pasos del proceso y, por lo mismo, no obtienen ningún resultado o el que obtienen es incorrecto.
Esta plantilla tiene la finalidad de guiar al alumno en el proceso de solución de problemas de
programación lineal por el método gráfico y permitir que el alumno se concentre en la aplicación de los
razonamientos necesarios para plantear el problema.
Los pasos que se recomiendan son:
1. Organizar los datos del problema.
2. Escribir las desigualdades que expresan las restricciones del problema.
2. En el mismo paso dos, se pide convertir las desigualdades en ecuaciones para graficarlas.
3. Trazar las rectas sobre un plano cartesiano que se incluye en el formato e identifica las áreas que representan el área de soluciones factibles.
4. Determina las coordenadas de los vértices que delimitan el área de soluciones factibles.
5. Obtén la función objetivo y sustituye los valores de las coordenadas de los vértices en dicha función objetivo.
6. Anota los resultados del problema tomando como base la interpretación del paso 5.
Esperamos que sea de utilidad.
Saludos.