Mostrando entradas con la etiqueta integral definida. Mostrar todas las entradas
Mostrando entradas con la etiqueta integral definida. Mostrar todas las entradas
viernes, 18 de febrero de 2022
miércoles, 16 de febrero de 2022
Definite Integral: Solids of Revolution
Integral Definida: Sólidos de Revolución
La integral definida es una excelente herramienta para resolver toda clase de problemas, uno de ellos, es el cálculo de volúmenes de revolución.
La presentación adjunta contiene una explicación detallada de la forma en que se aplica este conocimiento en la resolución de problemas.
Esperamos que sea de utilidad.
Saludos.
miércoles, 9 de febrero de 2022
Exercise 2.1. Area Under the Curve
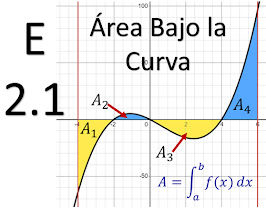
Ejercicio 2.1. Área Bajo la Curva
La práctica es la mejor forma de aprender matemáticas; en este ejercicio se practica el cálculo de áreas bajo la curva, poniendo especial atención a la necesidad de trazar la gráfica para identificar áreas positivas y negativas.
Esperamos que sea de utilidad.
Saludos.
martes, 19 de octubre de 2021
The Definite Integral 01
La Integral Definida 01
EL cálculo de áreas es un tema que ha sido abordado y resuelto por diferentes culturas desde hace miles de años, siempre que los límites de las figuras fueran líneas rectas.
Cuando alguno de los límites del área que se desea calcular es una curva, el procedimiento no resulta tan sencillo.
En la siguiente presentación se explica, paso a paso, el procedimiento para determinar el área limitada por el eje equis, una curva, y dos rectas verticales en valores específicos de equis.
Esperamos que sea de utilidad.
Saludos.
martes, 24 de marzo de 2020
Area Under the Curve (Part 2)
Area bajo la Curva, Segunda Parte
En una publicacipon anterior, que se encuentra en el enlace siguiente:http://proc-industriales.blogspot.com/2020/03/area-under-curve-part-1.html
Se explicó el procedimiento para obtener el átrea bajo la curva de una función que, en el intervalo que se desea calcular el área, está siempre por encima del eje equis, por lo que el área es positiva.
En clase obtuvimos el área mediante la calculadora, el resultado es el mismo que con el software Microsoft Mathematics.
El ejemplo que se resolvió en el pizarrón muestra el error que se genera cuando alguna parte del área se encuentra por encima del eje equis y otra, por debajo, ya que las áreas debajo del eje equis son negativas de modo que se restan del área positiva y se obtiene un resultado incorrecto.
El ejercicio consiste en:
Al resolverlo directamente nos encontramos con el resultado mostrado en el pizarrón y ahora obtenido mediante Microsoft Mathematics.
Y se explica que, para evitar cometer este error, es necesario identificar los puntos donde la curva corta al eje equis, en el ejemplo, uno de estos puntos se encuentra dentro del intervalo de integración, específicamente es el valor x = 1.53208888
En las gráficas se observan las dos áreas:
Negativa entre 1 y 1.53208888
Positiva entre 1.5320888 y 4
Estas dos integrales se resuelve por separado y se sus resultados se suman:
Este último valor es el resultado correcto de la integración.
Esperamos que sea de utilidad.
Saludos.
PD Si se desea acceder a la presentación del primer ejemplo puede emplearse el código QR.
Suscribirse a:
Entradas (Atom)
Artículos relacionados
