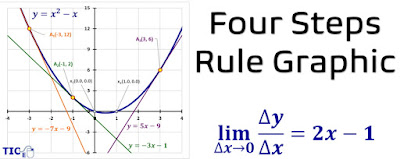
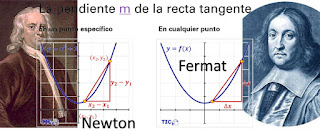
El desarrollo del cálculo tiene raíces desde la matemática griega, sin embargo, se consolida hasta el trabajo de Fermat en el que prácticamente utiliza el concepto de límite, y posteriormente con Newton y Leibnitz.
La presentación adjunta contiene una breve semblanza del proceso mediante el que se desarrolló el cálculo.
Esperamos que sea de utilidad.
Saludos.
Un antiguo problema del que se tiene evidencia de su estudio desde el periodo clásico griego, finalmente es resuelto mediante herramientas matemáticas recién inventadas.
Es le matemático Fermat quien propone un método de solución. En la presentación adjunta se plantea el uso del método empleado por Fermat aunque empleando solamente aritmética.
Esperamos que sea de utilidad.
Saludos.
El uso de formatos para al resolución y entrega de problemas, además de guiar al alumno hacia una forma ordenada de trabajo, permite dejar claro qué es lo que se espera que el alumno lleve a cabo para evidenciar sus competencias.
Al incluir el valor de cada paso del proceso promueve la autoevaluación como una forma de aprendizaje.
Esperamos que sea de utilidad.
Saludos.
La geometría es la primera rama de la matemática que se desarrollo hasta alcanzar su formalización en el libro de los elementos de Euclides.
Este desarrollo de la geometría tuvo como consecuencia que numerosos problemas de alto grado de dificultad fueron abordados y resueltos desde el siglo III a.C. Por casi 2000 años, el único libro de texto de matemáticas fueron los Elementos de Euclides.
En la guía didáctica anexa se propone el uso de la geometría analítica para el cálculo de pendiente de la recta tangente a una curva en un punto dado.
Esperamos que sea de utilidad.
Saludos.
La invención del cálculo diferencial se atribuye, casi universalmente, a Newton y Leibniz, sin embargo, cuarenta años antes de Newton, encontramos el método de las tangentes de Fermat que, de hecho, es una forma de cálculo diferencial. Tal vez por ello, Laplace afirmaba que el cálculo fue inventado por Fermat.
En la siguiente presentación se describe la forma de calcular la pendiente de una recta, dados dos puntos, y cómo esto conduce al desarrollo del trabajo de Fermat.
Esperamos que sea de utilidad.
Saludos.
