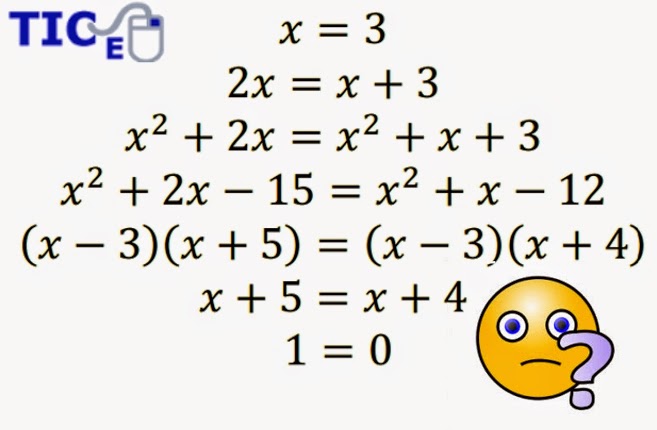Resolviendo problemas de integración fácilmente.
Las fórmulas o reglas de integración deben ser entendidas como reglas de aplicación, es decir, al observar una fórmula de integración debemos tomar en cuenta la estructura general de la fórmula, cuáles componentes deben aparecer y en que orden, para decidir si es problema que estamos revisando puede ser resuelto mediante una determinada fórmula.
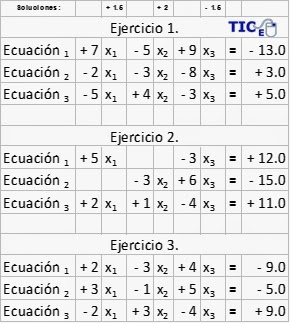
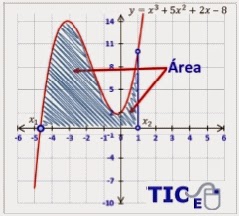
En este ejemplo se explica detalladamente el proceso de identificación y resolución del problema:
Como podemos observar, la expresión que se va a integrar no tiene la estructura de la fórmula que deseamos aplicar, por lo que es necesario emplear algunas propiedades algebraicas para acomodar los componentes de la expresión original y resolverla con la fórmula que se indica.
El proceso completo se encuentra en la siguiente presentación.
Esperamos que sea de utilidad.
Saludos.