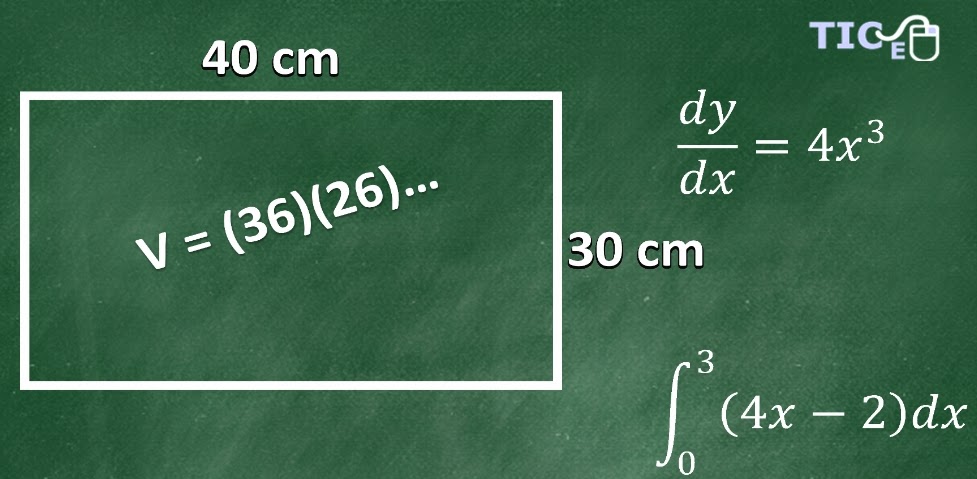Solving problems easily about derivative applications.

Resuelve fácilmente problemas acerca de aplicaciones de la derivada.

La derivada es una poderosa herramienta matemática. Nos permite enfrentar exitosamente problemas que, sin esta herramienta, pueden resultar demasiado complejos o, incluso, imposibles.

Entre las muchas aplicaciones de la derivada, la optimización a través del concepto de máximos y mínimos relativos, es una de las más comunes.

Como en casi todos los problemas de razonamiento, la obtención de la expresión algebraica que se va a derivar es lo más importante y, con frecuencia, lo más complejo.

Una estrategia para la resolución de estos problemas se basa en la identificación de la cantidad del problema cuyo valor podemos modificar arbitrariamente para que, a su vez, cambie el valor de otras cantidades y, al final, modifique la magnitud que se desea optimizar.

Ejemplo:

En este ejemplo se va a cambiar el tamaño de los cuadrados que se recortarán en las esquinas para observar como afecta a las dimensiones de la caja y, por lo tanto, al volumen que se desea maximizar.

La medida del lado de este cuadrado es equis, a partir de este valor, se determina la longitud, ancho y altura para calcular el volumen.

El procedimiento completo se encuentra en el siguiente enlace:

http://licmata-math.blogspot.mx/2014/10/solving-easily-famous-problem-of.html

Al realizar el análisis del problema, suelen producirse intentos, cálculos, gráficas, y otros recursos, a veces, desorganizados. Con la finalidad de ordenar el procedimiento y los productos mínimos que conducen al resultado, se propone el siguiente formato.

Esperamos que sea de utilidad.

Saludos.

Derivative applications Template from Matematica de Samos

Solving easily the famous problem of the paperboard box.

Resuelve fácilmente el famoso problema de la caja de cartón.

Los problemas de razonamiento pueden ser resueltos con facilidad, sólo es necesario desarrollar, aplicar y una mejorar poco a poco una estrategia para comprender dicho problema.

El famoso problema del que hablamos se encuentra en casi todos los libros de cálculo diferencial, probablemente con datos diferentes, corresponde al tema de máximos y mínimos.

La redacción del problema dice:

El procedimiento para resolver el problema pasa por las diversas herramientas que podríamos emplear: aritmética y geometría, álgebra, geometría analítica, para darnos cuenta que la herramienta apropiada es el cálculo diferencial.

Una explicación detallada del proceso de solución se encuentra en el siguiente archivo.

Aplicaciones de la derivada Maximizar volumen (Maximize volume) from Matematica de Samos

Calculus fundamentals.

Fundamentos del Cálculo (1).

El cálculo diferencial e integral se desarrollan a partir de necesidades prácticas y problemas que era necesario resolver. Parece lo más natural aprender el cálculo con esta perspectiva; partir de problemas que deben ser resueltos y, con base en esta necesidad, desarrollar los contenidos del curso.

El material anexo presenta este enfoque, se plantea un problema que, para resolverse, requiere el uso de aritmética, geometría, álgebra, razonamiento matemático, cálculo diferencial, máximos y mínimos relativos, entre otros.

Para un mejor aprovechamiento del material, es conveniente consultar los enlaces que se sugieren, como el formulario que se encuentra en este mismo blog:

http://licmata-math.blogspot.mx/p/liderazgo-y-autoridad.html

Esperamos que sea de utilidad.

Saludos.

Calculus fundamentals from Matematica de Samos

Problema resuelto de máximos y mínimos.

El problema de determinar las dimensiones de una caja sin tapa, con un material dado, con el objetivo de maximizar el volumen, es típico de las aplicaciones de la derivada.

El procedimiento de solución es relativamente sencillo cuando se emplea la derivada directamente, sin embargo, se desarrollan muchas más habilidades si se plantea el problema y se permite que el alumno trate de resolverlo con las herramientas que conoce.
Desde el momento que se presenta el problema al grupo, se promueve la discusión y la participación preguntando, por ejemplo, si creen que el volumen de la caja será diferente según el tamaño del cuadrado que se recorte. Generalmente se forman dos grupos; uno de ellos afirma que el volumen es el mismo, ya que se usa el mismo material y se “compensa” la mayor altura de una de las cajas con el mayor ancho de la otra, y otro, que considera que si habrá cambio en el volumen ya que se recorta una mayor o menor cantidad de material.

En la siguiente presentación se resume el proceso seguido con lo estudiantes.

Aplicaciones de la derivada Maximizar volumen (Maximize volume) from Matematica de Samos

Para fines de evaluación y organización de la información, se sugiere el uso de un formato que permita observar los procesos intelectuales del alumno, como el siguiente.

Maximos y minimos maximize box volume from Matematica de Samos

En este mismo blog se encuentra un formulario de matemáticas básicas conteniendo las fórmulas de derivación e integración, y algunos fundamentos de álgebra y trigonometría. 

Saludos.

Máximos y mínimos relativos de una función.

Aplicaciones de la derivada.

Existen numerosos problemas en los que el objetivo es optimizar un valor; puede tratarse de maximizar rendimientos y ganancias, o de minimizar costos o desperdicio. En general son problemas en los que se trata de determinar el valor máximo o mínimo de una función.

Algunos ejemplos de este tema pueden encontrarse en este mismo blog:
http://licmata-math.blogspot.mx/2011/11/aplicaciones-de-la-derivada.html
http://licmata-math.blogspot.mx/2012/10/aplicaciones-de-la-derivada.html
http://licmata-math.blogspot.mx/2012/01/aplicaciones-de-la-derivada-2.html

Para resolver estos problemas es necesario, en primer lugar, analizar y plantear el problema, lo cuál significa obtener la ecuación que se va a derivar. Conforme al modelo de educación basada en competencias, es mucho más importante el proceso que se sigue para resolver el problema, que la solución misma, por ello, se propone el siguiente formato, con la finalidad de mostrar, detalladamente, el proceso que se siguió para obtener la ecuación, así como la solución del problema.

Esperamos que sea de utilidad.

Unidad 3 formato 15-aplicaciones derivada-2 from Matematica de Samos

Aplicaciones de la derivada.

Máximos y mínimos relativos de una función.

Una de las aplicaciones más interesantes del cálculo diferencial son los problemas de optimización que pueden ser resueltos mediante los conceptos de máximos y mínimos relativos de una función. Son problemas de razonamiento que se resuelven derivando e igualando a cero la función que describe el comportamiento del fenómeno en estudio. Es necesario leer detenidamente el problema para determinar la función que se va a derivar.

Ejemplo:

Se dispone de una pieza rectangular de cartón que mide 40 x 30 centímetros. Con este material se fabricará una caja sin tapa, recortando en las 4 esquinas, cuadrados de la misma medida y recortando la pieza resultante como se muestra en la figura.

En el siguiente archivo se encuentra un formato para resolver problemas de máximos y mínimos relativos de una función.

Saludos.

Unidad 3 formato 15-aplicaciones derivada from Matematica de Samos