Rúbrica para evaluar problemas de razonamiento 2.

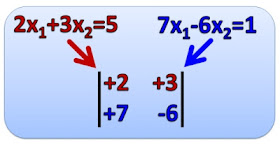
La siguiente rúbrica es el instrumento que se utilizará para evaluar el proceso de planteamiento de problemas de razonamiento que se resolverán mediante sistemas de dos ecuaciones con dos incógnitas.

Está ligado al formato que se emplea para plantear problemas de razonamiento mediante sistemas de do ecuaciones con dos incógnitas que se encuentra en este mismo blog (http://licmata-math.blogspot.mx/2012/10/sistemas-de-2-ecuaciones-con-2.html).

Está diseñado para que un problema completo, planteado correctamente, tenga un valor de 20 puntos.

Saludos.

Rúbrica problemas razonamiento 2 incógnitas from Matematica de Samos

Problemas de razonamiento, tres incógnitas.

Los problemas de razonamiento presentan un especial grado de dificultad a los estudiantes de todos los niveles escolares.

La resolución de dichos problemas requiere de un análisis cuidadoso de la información y luego, de una traducción entre el lenguaje natural y el algebraico. En este formato, se separan las diferentes habilidades y se evalúan mediante una rúbrica para señalar con la mayor precisión posible, las áreas de oportunidad del alumno.

El planteamiento de estos problemas puede realizarse mediante una ecuación de primer grado con una incógnita, dos ecuaciones lineales con dos incógnitas, tres, hasta "n" ecuaciones con "n" incógnitas.

En el archivo siguiente se encuentra un formato para plantear problemas de razonamiento mediante tres ecuaciones con tres incógnitas. Una vez generado el sistema de ecuaciones que describe el problema, puede ser resuelto por cualquier método: Gauss, Matriz inversa, Gauss Jordan, Reducción, Cramer, entre otros.

Saludos.

Unidad 2 formato 7-razonamiento tres incógnitas from Matematica de Samos

Aplicaciones de la derivada.

Máximos y mínimos relativos de una función.

Una de las aplicaciones más interesantes del cálculo diferencial son los problemas de optimización que pueden ser resueltos mediante los conceptos de máximos y mínimos relativos de una función. Son problemas de razonamiento que se resuelven derivando e igualando a cero la función que describe el comportamiento del fenómeno en estudio. Es necesario leer detenidamente el problema para determinar la función que se va a derivar.

Ejemplo:

Se dispone de una pieza rectangular de cartón que mide 40 x 30 centímetros. Con este material se fabricará una caja sin tapa, recortando en las 4 esquinas, cuadrados de la misma medida y recortando la pieza resultante como se muestra en la figura.

En el siguiente archivo se encuentra un formato para resolver problemas de máximos y mínimos relativos de una función.

Saludos.

Unidad 3 formato 15-aplicaciones derivada from Matematica de Samos

Método de Cramer 3x3

Solución de sistemas de 3 ecuaciones lineales con 3 incógnitas por el método de Cramer o por determinantes.

El método de Cramer o por determinantes es muy sencillo aunque laborioso. Para el caso de tres incógnitas, en ocasiones es preferible a los métodos como Gauss, Gauss Jordan y matriz inversa debido a su sencillez.

El siguiente formato tiene la finalidad de guiar el procedimiento y ordenar todos los pasos de modo que sea poco probable que se cometan errores por falta de orden en la escritura de los números.

Esperamos que sea de utilidad.

Saludos.

Unidad 2 formato 8 - cramer3x3 from Matematica de Samos

Gauss Jordan solver.

Existen muchas páginas en internet que contienen programas, generalmente desarrollados en lenguaje java, capaces de resolver sistemas de ecuaciones lineales por el método de Gauss Jordan, incluso muchas de ellas muestran el procedimiento de solución.

Aunque pueden estar en inglés, son muy fáciles de usar, si usamos un traductor, no tendremos problemas para entenderlas.

Algunas de dichas páginas son:

http://www.scoop.it/t/mathematics-learning

http://www.idomaths.com/gauss_jordan.php

http://matrix.reshish.com/gauss-jordanElimination.php

http://calculator.tutorvista.com/gauss-jordan-elimination-calculator.html#

Generalmente la resolución de estos sistemas no ofrece mayores dificultades, lo interesante es el planteamiento de los problemas de dónde se obtienen estos sistemas de ecuaciones.

Saludos.

Gauss Jordan 4x4.

Método de Gauss Jordan para resolver sistemas de 4 ecuaciones lineales con 4 incógnitas.

El método comienza con la matriz aumentada del sistema, que es la que se utilizó como encabezado de esta entrada.

El proceso de reducción inicia obteniendo uno en el coeficiente de la primera incógnita de la primera ecuación y ceros debajo de ella, el resto de los números no importan.

A continuación se obtiene uno en el coeficiente de la segunda incógnita en la segunda ecuación y ceros arriba y abajo de él.

A continuación se obtiene uno en el coeficiente de la tercera incógnita de la tercera ecuación y cros arriba y abajo de él.

Finalmente se obtiene uno en el coeficiente de la cuarta incógnita de la cuarta ecuación y ceros arriba de él.

En esta última matriz pueden leerse directamente los valores de las incógnitas en la columna de términos independientes.

En el siguiente archivo se encuentra un formato para resolver ordenadamente un sistema de 4 ecuaciones lineales con 4 incógnitas por el método de Gauss Jordan.

Saludos.

Formato gauss jordan 4x4 from Matematica de Samos

Gauss 4 incógnitas

El método de Gauss para la resolución de sistemas de 4 ecuaciones  lineales con 4 incógnitas.

Cuanto más grande es el sistema de ecuaciones, más conveniente resulta este método, ya que el de Cramer se vuelve extremadamente ineficiente a partir de 4 ecuaciones con 4 incógnitas.Una posible opción sería el método de Gauss Jordan.

En el siguiente archivo se encuentra un formato que tiene la finalidad de organizar el procedimiento de solución, ya que en este método el orden es muy importante; con frecuencia se cometen errores porque los números están mal escritos o desordenados.

Esperamos que sea de utilidad.

Saludos.

Formato gauss 4x4 from Matematica de Samos

Gauss Jordan 3 ecuaciones.

El método de Gauss Jordan mejora el de Gauss en el sentido de evitar el álgebra.
En el siguiente archivo se encuentra un formato para resolver ordenadamente un sistema de 3 ecuaciones con 3 incógnitas por el método de Gauss Jordan.

Formato gauss jordan 3x3 from Matematica de Samos

Sistemas de 'n' ecuaciones con 'n' incógnitas

En los siguientes archivos se encuentran sistemas de 4, 5, 6, 7, 8, 9 y 10 ecuaciones. Selecciona y resuelve el que corresponde a tu número de lista empleando el método de Cramer con Excel.


http://www.4shared.com/office/m2g3De5H/Sistemas_de_4x4.html
http://www.4shared.com/office/hj0_JtBt/Sistemas_de_5x5.html
http://www.4shared.com/office/0Yk6_WzQ/Sistemas_de_6x6.html
http://www.4shared.com/office/Gd6VNmxK/Sistemas_de_7x7.html
http://www.4shared.com/office/EsEryLVW/Sistemas_de_8x8.html
http://www.4shared.com/office/itQqfy_B/Sistemas_de_9x9.html
http://www.4shared.com/office/kOts_1F6/Sistemas_de_10x10.html


Saludos.

Método de Gauss.

El método de Gauss para la resolución de sistemas de 3 ecuaciones  lineales con 3 incógnitas.

El método de Gauss es mucho más eficiente que el de Cramer, el problema que a veces se presenta es la necesidad de utilizar fracciones comunes, sin embargo, estas operaciones pueden ser efectuadas con la calculadora.

En el siguiente archivo se encuentra un formato que tiene la finalidad de organizar el procedimiento de solución, ya que en este método el orden es muy importante; con frecuencia se cometen errores porque los números están mal escritos o desordenados.

Esperamos que sea de utilidad.

Saludos.

Formato gauss 3x3 from Matematica de Samos

Apuntes de álgebra. Parte 3.

Tercera parte de los apuntes de álgebra.

En estos apuntes se encuentra información acerca de sistemas de 3 ecuaciones con 3 incógnitas resueltos por el método de Cramer o determinantes. También incluye problemas de razonamiento con tres incógnitas.

Las partes anteriores se encuentran en este mismo blog en los enlaces siguientes:

http://licmata-math.blogspot.mx/2012/08/apuntes-de-algebra.html
http://licmata-math.blogspot.mx/2012/09/apuntes-de-algebra-segunda-parte.html

Saludos.

Enlace al archivo:

http://www.4shared.com/office/zWr2PsDf/matemticas_U2Ecuaciones_Algebr.html

Método de Cramer - Determinantes en Excel

Los sistemas de dos ecuaciones con dos incógnitas pueden ser fácilmente resueltos, se acostumbra emplear; el método gráfico, de reducción, de sustitución o de igualación, sin embargo, tal vez resulte más sencillo resolverlos por el método de Cramer.

En el siguiente archivo se encuentra una hoja de cálculo en Excel que resuelve sistemas de dos ecuaciones con dos incógnitas por determinantes.

hace falta ajustarlo un poco para que indique cuando el sistema no tiene solución o tiene infinidad de soluciones.

Esperamos que sea de utilidad.

Punto de equilibrio - problema resuelto

Existen muchas aplicaciones de los sistemas de ecuaciones lineales, en este ejemplo se resuelve la primera parte de un problema de punto de equilibrio, específicamente se determina dicho punto resolviendo, por el método gráfico, un sistema de dos ecuaciones con dos incógnitas.

El problema propuesto es:

En la fábrica de computadoras HAL se incurre en costos fijos de $750,000 mensuales para fabricar el modelo Netbook-2012, la cuál tiene un costo unitario de manufactura de $2,800.

Si cada unidad se vende al distribuidor en $3,500, ¿cuál es el punto de equilibrio?

La imagen que encabeza esta entrada muestra cómo queda la solución utilizando Excel para la elaboración de la gráfica.

Presentación conteniendo el proceso de solución.

Punto de equlibrio 2 ecuaciones 2 incógnitas from Matematica de Samos

Método de sustitución.

Una actividad que, por el momento, no pueden realizar la computadoras, es el planteamiento de problemas. Tampoco existen formularios para esta actividad. Muchos de estos planteamientos conducen a sistemas de dos ecuaciones con dos incógnitas que pueden ser resueltos por diversos métodos.

En el siguiente archivo se encuentra un formato (template o plantilla), que tiene la finalidad de organizar el proceso de solución de sistemas de 2x2.

Esperamos que sea útil.

Saludos.

Unidad 2 formato 6-método sustitución from Matematica de Samos

Método de reducción o suma y resta.

Al plantear un problema de razonamiento surge un sistema de dos ecuaciones con dos incógnitas, para resolverlo existen varios métodos. El siguiente formato sirve para presentar ordenadamente el proceso de solución de un sistema de dos ecuaciones con dos incógnitas por el método de reducción o suma y resta.

Esperamos que sea de utilidad.

Saludos.

Unidad 2 formato 5-método reducción from Matematica de Samos

.

Método de igualación.

Los sistemas de dos ecuaciones con dos incógnitas surgen del planteamiento de los problemas de razonamiento.

Independientemente de dónde se origine un sistema de dos ecuaciones lineales con dos incógnitas, existen varios métodos para resolverlo. En la entrada anterior está el formato para resolverlo por el método gráficos. En el siguiente archivo está un formato para resolverlo por el método de igualación.

Unidad 2 formato 4-método igualación from Matematica de Samos

Sistemas de 2 ecuaciones con 2 incógnitas

Los sistemas de dos ecuaciones con dos incógnitas se generan al tratar de resolver algunos problemas de razonamiento. En los siguientes archivos se encuentran dos formatos: uno de ellos para registrar el procedimiento mediante el cuál se planteó el sistema de dos ecuaciones, y el otro para tabular y trazar las gráficas que nos permitirán obtener la solución.

Unidad 2 formato 2-problemas dos incógnitas from Matematica de Samos

Unidad 2 formato 3-método gráfico from Matematica de Samos